Metode Pencarian: Blind and Heuristic

Dalam post kali ini penulis akan membahas tentang metode pencarian buta (blind search) dan heuristik (heuristic search).

A. Metode Pencarian Buta

Secara umum metode pencarian buta didefinisikan sebagai sebuah metode pencarian pada sistem berbasis kecerdasan buatan yang didesain untuk tidak memiliki informasi awal pada sistemnya. Sebagai gantinya, metode ini hanya memiliki kemampuan untuk membedakan sebuah tujuan dengan hal-hal lainnya yang bukan bersifat sebagai tujuan. Hal ini dikarenakan sistem hanya bertugas untuk mencari sesuatu di dalam sebuah pohon pencarian, dengan cara yaitu membuka tiap titik (node) yang ada pada tiap tingkatan (level) dari pohon tersebut. Adapun sebuah titik pada pohon pencarian melambangkan sebuah kondisi, dengan sebagian di antara kumpulan titik pada pohon tersebut merupakan tujuan pencarian dari metode pencarian buta tersebut (walaupun terkadang pada pohon tersebut semua titik yang ada tidak berisi titik tujuan pencarian oleh sistem). Sejatinya pohon pencarian merupakan lambang dari area pencarian yang disasar oleh sistem, dimana hal ini untuk mempermudah proses pencarian node tujuan dengan cara menyusunnya menjadi sebuah pohon yang dapat ditelusuri oleh sistem dengan mudah.

Ada beberapa jenis algoritma yang tergolong sebagai bagian dari metode pencarian buta, namun dua di antaranya adalah algoritma untuk metode pencarian buta yang paling banyak dipergunakan, yaitu:

1. Breadth First Search (BFS)

Penggambaran struktur graf pohon untuk algoritma BFS | Sumber: https://en.wikipedia.org/wiki/Breadth-first_search

Konsep paling awal dari algoritma ini pertama kali dikonsepkan oleh Konrad Zuse pada tahun 1945 dalam tesis Ph.Dnya pada bahasa pemrograman Plankalkül (Formal System for Planning) yang dimana pada konsep yang dikemukakan oleh Zuse tersebut algoritma ini ditujukan sebagai sebuah cara untuk menelusuri komponen yang saling terhubung pada sebuah graf. Konsep algoritma ini kemudian disempurnakan oleh Edward F. Moore untuk pencarian jalan paling singkat untuk keluar dari sebuah labirin. Secara sederhana proses pencarian simpul graf dengan menggunakan algoritma BFS menggunakan teknik non-rekursif, dengan proses yang dilakukan yaitu:

1. Kunjungi simpul paling awal dari graf
2. Setelahnya kunjungi simpul yang bertetangga dengan simpul paling awal tersebut
3. Jika ada simpul yang belum dikunjungi dan bertetangga dengan simpul yang sudah dikunjungi, kunjungi simpul tersebut hingga semua simpul telah dikunjungi

Namun apabila graf tersebut berbentuk pohon yang memiliki akar, maka prosesnya menjadi:

1. Kunjungi simpul akar dari graf
2. Setelahnya kunjungi simpul cabang yang ada di satu tingkat lebih tinggi dari simpul akar
3. Jika ada simpul yang belum dikunjungi dan berada di satu tingkat yang lebih tinggi dari tingkatan simpul yang sudah dikunjungi, kunjungi simpul tersebut hingga semua simpul telah dikunjungi

Karena umumnya graf direpresentasikan sebagai sebuah array berbentuk antrian (queue), maka secara umum operasi pengunjungan simpul pada graf dengan menggunakan algoritma BFS dilakukan dengan cara yaitu menelusuri masing-masing elemen data pada array graf tersebut secara keseluruhan. Selain menggunakan array antrian, algoritma BFS juga menggunakan linked list sebagai media penggambaran dari graf yang isinya akan ditelusuri satu per satu untuk mencari simpul tujuan dari graf tersebut. Namun pada dasarnya penggunaan array maupun linked list dalam algoritma BFS sama-sama menggambarkan bahwa operasi dari algoritma tersebut akan menelusuri masing-masing elemen dalam sebuah graf untuk mencapai elemen tujuan tanpa mengetahui elemen apa yang akan dilalui selama mencari jalan tersingkat menuju elemen tujuan tersebut.

Contoh dari pengaplikasian BFS dalam pemecahan suatu masalah yaitu pada kasus pencarian rute angkutan umum dari suatu lokasi ke lokasi lainnya. Pada kasus ini titik awal pencariannya adalah Terminal Senen, dengan titik akhirnya yaitu Terminal Kampung Rambutan. Prosesnya yaitu:

1. Kunjungi titik Terminal Senen.
2. Setelahnya bangkitkan simpul cabang dari titik Terminal Senen yaitu Blok M, Pulo Gadung dan Manggarai, lalu kunjungi simpul cabang tersebut.
3. Karena titik tujuan belum tercapai, maka bangkitkan simpul cabang dari masing-masing simpul cabang yang telah dikunjungi pada tahap nomor 2, yaitu Grogol, Lebak Bulus, Bekasi, Cililitan dan Harmoni.
4. Dikarenakan titik tujuan masih belum tercapai, bangkitkan simpul cabang dari masing-masing simpul cabang yang telah dikunjungi pada tahap nomor 3 yaitu Kalideres, Ciputat, Kampung Rambutan, Kota dan Tanah Abang.
5. Pada tahap ini titik tujuan (yaitu Kampung Rambutan) sudah ditemukan, sehingga proses selesai.

Di sini sistem tidak mengetahui isi dari titik cabang untuk Terminal Senen, sehingga sistem akan terlebih dahulu membuka lalu mengunjungi masing-masing titik cabang tersebut dengan menggunakan algoritma BFS untuk mengetahui isi dari titik selanjutnya. Ketika dibuka dan dikunjungi, ternyata isinya adalah Terminal Blok M, Terminal Pulo Gadung dan Terminal Manggarai. Maka di sini sistem akan mengulangi prosesnya untuk mengetahui isi dari titik selanjutnya. Proses ini terus dilakukan hingga akhirnya sistem menemukan salah satu titik cabang dari titik cabang yang telah dikunjungi pada tahap sebelumnya adalah titik tujuannya yaitu Terminal Kampung Rambutan. Kemampuan untuk membedakan titik tujuan dari titik bukan tujuan sangatlah dibutuhkan karena hal ini digunakan untuk mencegah sistem menemui kebuntuan ketika mencari titik tujuan.

2. Depth First Search (DFS)

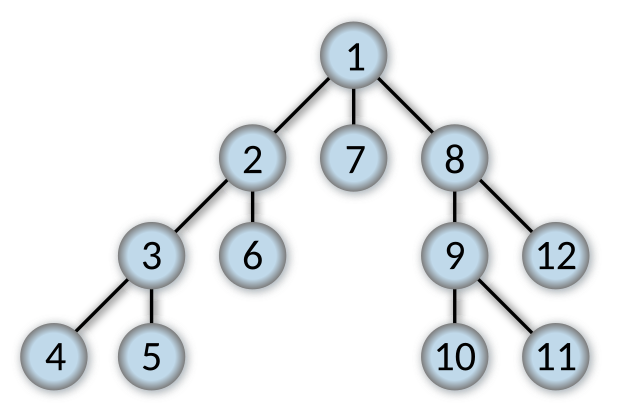Penggambaran struktur graf pohon untuk algoritma DFS | Sumber: https://en.wikipedia.org/wiki/Depth-first_search

Algoritma ini pada dasarnya memiliki kesamaan struktur dengan algoritma BFS, dimana sistem akan mencari titik tujuan dengan mengunjungi semua titik pada satu tingkat sebelum kemudian beranjak ke tingkat selanjutnya untuk mengunjungi titik lainnya hingga titik tujuannya berhasil ditemukan. Namun perbedaannya adalah algoritma DFS bekerja dengan cara yang terbalik dibanding dengan BFS, dimana algoritma DFS menerapkan prinsip berupa penelusuran dari tingkat pertama langsung ke titik paling kiri dari tingkat selanjutnya. Adapun cara kerjanya yaitu sistem terlebih dahulu mengunjungi titik paling kiri dari tingkat selanjutnya pada graf untuk mencari titik tujuannya. Jika pada posisi tersebut titik tujuannya tidak ditemukan, maka sistem kemudian mencari hingga ke titik paling kiri dari tingkat terdalam. Apabila tidak juga ditemukan, maka penelusuran akan dilakukan dari titik sebelah kanannya. Proses ini dilanjutkan secara berulang hingga titik tujuan ditemukan oleh sistem. Jika titik tujuannya sudah ditemukan, maka proses backtracking yang berfungsi untuk menelusuri balik untuk mendapatkan jalur yang diinginkan tidak perlu dilakukan.

DFS secara umum hanya membutuhkan memori yang sedikit untuk melakukan proses penelusuran sebuah graf secara keseluruhan. Hal ini dikarenakan DFS hanya akan menyimpan titik yang terdapat di lintasan yang aktif saja. Selain itu apabila titik tujuannya berada di posisi paling kiri yang pertama kali ditelusuri maka sistem dapat langsung mengakhiri proses pencariannya tanpa perlu menelusuri titik lainnya dalam graf. Ini tentunya berbeda dengan BFS yang harus menyimpan semua titik yang telah dibangkitkan dan dikunjungi dalam graf, yang dimana ini membebani kinerja memori. Maka dapat dikatakan bahwa algoritma DFS bekerja secara lebih cepat dibandingkan dengan BFS. Namun kelemahannya adalah DFS berpotensi tidak mampu bekerja dengan baik jika berhadapan dengan graf yang jumlah tingkatannya sangat banyak. Bahkan algoritma DFS sendiri juga berpotensi untuk tidak menemukan titik tujuan yang diharapkan.

Contoh pengaplikasian dari algoritma DFS dalam suatu kasus pada dasarnya sama dengan yang ada di algoritma BFS, namun untuk lebih detailnya ada suatu kasus berupa penggunaan algoritma DFS untuk pembuatan aplikasi yang membantu pencarian rute bus terpendek di wilayah kota Solo. Pada kasus ini terdapat banyak bus kota yang beroperasi di dalam wilayah kota Solo, dengan pengoperasian masing-masing trayek dilakukan oleh perusahaan yang berbeda dan rute dari trayeknya berbeda pula. Ini tentunya menyulitkan semua orang yang ingin menggunakan jasa angkutan bus di Solo, sehingga dari sini lahirlah ide pembuatan aplikasi tersebut. Secara singkat pola kerja algoritma DFS pada aplikasi tersebut yaitu mencari rute bus mana yang paling pendek untuk mencapai suatu tempat. Misalkan titik awal pencarian adalah di daerah Palur, sedangkan titik tujuannya yaitu Pasar Klewer. Ada 2 rute bis yang dioperasikan oleh perusahaan yang berbeda, dengan proses penelusurannya yaitu sebagai berikut:

1. Kunjungi Palur sebagai titik awal pada graf rute.
2. Selanjutnya bangkitkan dan kunjungi Panggung sebagai titik selanjutnya pada graf tersebut.
3. Kemudian bangkitkan dan kunjungi Stasiun Solo Balapan sebagai titik selanjutnya. Karena di sini tidak ditemukan titik tujuan yaitu Pasar Klewer, maka proses penelusuran dikembalikan ke titik sebelumnya (Panggung) untuk berpindah ke rute selanjutnya.
4. Hapus titik Solo Balapan dari memori. Dari Panggung penelusuran diarahkan ke titik yang berada di sisi kanan graf rute yaitu Pasar Gede. Bangkitkan dan kunjungi titik tersebut.
5. Pada tahap ini bangkitkan dan kunjungi titik selanjutnya. Di sini titik selanjutnya adalah titik tujuan yaitu Pasar Klewer, maka proses penelusuran selesai.

B. Metode Pencarian Heuristik

Metode ini didefinisikan sebagai sebuah teknik pencarian yang didesain untuk menemukan suatu solusi pemecahan masalah secara cepat dan efisien tanpa harus menghabiskan banyak waktu dalam pelaksanaan prosesnya. Umumnya pemecahan masalah yang membutuhkan penggunaan komputer diselesaikan dengan program yang memanfaatkan teknik konvensional seperti pemrograman linear, pemrograman dinamis dan sebagainya. Namun teknik pencarian berbasis heuristik memungkinkan adanya pemecahan terhadap suatu masalah yang tidak dapat diselesaikan dengan teknik konvensional karena berbagai hal yang membuat teknik konvensional tidak dapat memecahkan masalah tersebut, salah satunya seperti tingginya tingkat kerumitan dari masalah tersebut. Meskipun tidak ada jaminan bahwa hasil pencariannya akan sangat lengkap atau optimal sesuai dengan harapan dari pengguna, namun teknik heuristik mampu menghasilkan solusi yang konkrit untuk memecahkan masalah skala besar secara adaptif dan dapat menggunakan modul tambahan dalam mengakses informasi yang berkaitan dengan pemecahan masalah tersebut. Selain itu teknik heuristik biasanya didukung dengan penggunakan antarmuka pengguna yang berbasis grafis (GUI) untuk memudahkan pengguna dalam memahami hasil pencariannya. Bahkan penggunaan teknik heuristik dalam proses pemecahan suatu masalah sendiri memungkinkan didapatnya lebih dari satu solusi untuk memecahkan satu masalah saja, yang dimana ini menandakan teknik heuristik memiliki fleksibilitas yang tinggi.

Seperti halnya metode pencarian buta, terdapat beberapa jenis algoritma dari metode pencarian heuristik. Namun yang akan dibahas dalam artikel ini hanyalah algoritma Generate and Test dan Hill Climbing saja. Pembahasan dari masing-masing algoritma tersebut adalah sebagai berikut:

1. Generate and Test

Secara umum algoritma ini akan melakukan pencarian terhadap suatu solusi dengan memfokuskan pada pencarian solusi yang mungkin untuk dapat dipergunakan dalam memecahkan suatu masalah. Pola dari pencariannya sendiri yaitu membangkitkan suatu kemungkinan solusi (yang pada dasarnya adalah titik dalam suatu graf) untuk kemudian diuji apakah isinya sesuai dengan tujuan yang diharapkan atau tidak. Algoritma ini menjamin ditemukannya solusi yang diharapkan jika prosesnya dilakukan secara sistematis. Tetapi apabila ruang lingkup kerja (graf) yang ditelusuri tersebut sangat luas, maka prosesnya akan membutuhkan waktu yang sangat lama untuk menyelesaikannya. Adapun algoritma ini menggunakan salah satu prinsip dasarnya yaitu dari algoritma Depth-First Search (DFS), dimana prinsipnya dipergunakan untuk proses pembangkitan solusi yang hanya membutuhkan penggunaan memori yang sedikit. Sedangkan untuk proses pengujiannya sendiri menggunakan metode backtracking untuk memastikan apakah solusinya sesuai dengan harapan atau tidak. Secara lengkap pola berikut menggambarkan bagaimana cara kerja dari algoritma Generate and Test ketika mencari solusi (titik tujuan):

1. Bangkitkan suatu kemungkinan solusi yang ditemukan.
2. Ujicoba apakah yang telah dibangkitkan adalah benar-benar solusi dengan membandingkan titik yang diuji dengan tujuan yang diharapkan.
3. Jika yang dibangkitkan merupakan solusi, akhiri proses dan keluar dari sistem. Jika solusi belum ditemukan, ulangi prosesnya ke langkah 1.

Salah satu contoh kasusnya adalah Travelling Salesman Problem (TSP), dimana dalam kasus tersebut diceritakan bahwa seorang salesman ditugaskan untuk mengunjungi beberapa kota sebanyak n. Adapun persyaratan yang ditetapkan adalah sang salesman hanya boleh mengunjungi tiap kota sebanyak sekali, dan yang ingin diketahui adalah rute terpendek yang mampu menghubungkan tiap kota tanpa harus melewati salah satu kota sebanyak dua kali atau lebih. Untuk itu dilakukanlah proses pencarian dengan menggunakan algoritma Generate and Test. Sebagai contoh yaitu ada empat kota yang harus dikunjungi, yaitu kota A, kota B, kota C dan kota D. Jika digambarkan sebagai sebuah graf, maka tiap ruas penghubung masing-masing titik (yang merupakan analogi untuk jarak dari rute antar tiap kota) dalam graf tersebut yaitu:

Graf analogi untuk rute penghubung antar kota | Sumber: http://fryunfirst.blogspot.co.id/2015/06/pencarian-heuristik-heuristic-search.html

Jika ditelusuri dengan menggunakan algoritma ini, maka ada beberapa rute yang memungkinkan untuk diambil pada tiap langkah pencarian, yaitu:

1. ABCD (jarak: 19) - rute terpilih: ABCD (jarak: 19)
2. ABDC (jarak: 18) - rute terpilih: ABDC (jarak: 18)
3. ACBD (jarak: 12) - rute terpilih: ACBD (jarak: 12)

Dari tiap langkah pencarian tersebut dipilihlah rute yang jaraknya paling pendek yaitu ACBD dengan jarak yang harus ditempuh sebanyak 12. Ini dikarenakan berdasarkan pembandingan kemungkinan solusi yang ditemukan dari tiap langkah pencarian tersebut didapat hasil yang menyatakan bahwa dari semua pilihan rute yang ada jarak yang paling pendek untuk ditempuh antara tiap kota adalah rute ACBD. Bila dibandingkan dengan rute lainnya seperti ABCD (19), ABDC (18), ACDB (13) dan sebagainya, rute ACBD inilah yang paling pendek, sehingga ditarik kesimpulan bahwa untuk kasus TSP ini rute yang paling direkomendasikan untuk penyelesaian masalah tersebut adalah rute ACBD, karena rute tersebut memenuhi persyaratan berupa "rute yang diambil haruslah rute terpendek tanpa perlu melewati salah satu kota lebih dari satu kali". Adapun gambar contoh untuk graf pohon yang berfungsi untuk membantu penyelesaian masalah tersebut adalah pada gambar berikut:

Graf pohon untuk penyelesaian kasus TSP | Sumber: https://amandainhere.blogspot.co.id/2016/11/contoh-pencarian-generate-and-test.html

2. Hill Climbing

Berdasarkan strukturnya algoritma ini merupakan variasi dari algoritma Generate and Test yang telah dijelaskan sebelumnya. Karena itulah antara kedua algoritma tersebut terdapat beberapa kesamaan, salah satunya yaitu penggunaan algoritma DFS sebagai basis dasar dari pengembangan algoritma berbasis heuristik. Namun terdapat pula beberapa perbedaan mekanisme yang muncul di antara kedua algoritma tersebut, dengan salah satu perbedaan yang paling mencolok dari algoritma Hill Climbing adalah pada penggunaan teknik heuristik untuk proses pengujian hasil terkaan terhadap suatu titik yang dianalisa oleh sistem. Penggunaan teknik heuristik dalam pengujian hasil terkaan ini adalah dalam rangka untuk menguji seberapa baiknya nilai terkaan yang telah didapat dari hasil pencarian terhadap keadaan yang dibangkitkan dalam proses iterasi yang dilakukan pada algoritma tersebut. Untuk proses pembangkitan dari keadaan berikutnya sendiri semuanya bergantung kepada umpan balik dari prosedur pengujian yang dilakukan pada keadaan sebelumnya.

Pola kerja dari algoritma hill climbing adalah:

1. Definisikan sebuah keadaan sebagai titik awal.
2. Terapkan sebuah operasi pada keadaan saat ini dan ambil sebuah keadaan baru sebagai titik berikutnya.
3. Bandingkan keadaan baru yang telah didapat dengan titik tujuan. Jika titik tujuan telah tercapai, maka akhiri operasi ini. Jika tidak tercapai, maka lakukan langkah 4.
4. Lakukan evaluasi terhadap keadaan baru tersebut dengan fungsi heuristik, kemudian lakukan pembandingan dengan keadaan yang sekarang. Jika keadaan baru yang dibandingkan tersebut mendekati dengan titik tujuan dibandingkan dengan keadaan yang sekarang, maka perbarui keadaan sekarang tersebut.

Untuk algoritma ini, contoh kasusnya yaitu pada penyusunan isi suatu stack dari yang semula tidak beraturan menjadi terurut, dengan kondisi awal dan kondisi yang dijadikan tujuan adalah seperti pada gambar berikut ini:

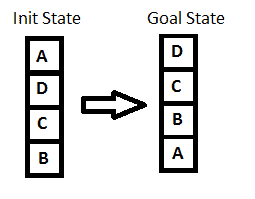Kondisi awal dan kondisi tujuan dari penyusunan stack | Sumber: http://www.baeldung.com/wp-content/uploads/2017/06/init_goal.png

Proses penyelesaiannya yaitu:

1. Keluarkan elemen A yang terletak pada posisi paling atas (top) dari stack. Pada posisi ini elemen top berubah dari elemen A menjadi elemen D. Ulangi langkah ini hingga semua elemen telah dikeluarkan dari dalam stack tersebut, dengan elemen B sebagai elemen terakhir yang dikeluarkan dari stack tersebut adalah elemen yang terletak di dasar stack.
2. Selanjutnya pilih elemen A sebagai elemen dasar baru dari stack, lalu masukkan ke dalam stack. Kemudian pilih B sebagai elemen top dari stack, dan masukkan ke dalam stack. Ulangi prosesnya hingga elemen D (sebagai elemen final) dimasukkan ke dalam stack. Kemudian tetapkan elemen D sebagai elemen top dari stack tersebut.

Apabila dijelaskan berdasarkan gambar maka polanya menjadi:

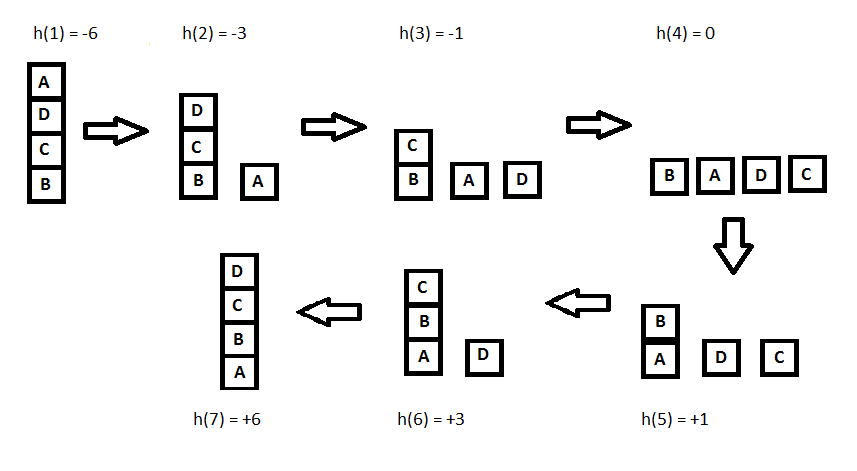Pola penyelesaian operasi pengurutan data pada stack dengan menggunakan algoritma hill climbing | Sumber: http://www.baeldung.com/wp-content/uploads/2017/06/state_iterations.png

C. Sumber

1. Kendall, Graham. 2001. G5AIAI - Introduction to Artificial Intelligence. http://www.cs.nott.ac.uk/~pszgxk/courses/g5aiai/003blindsearches/blind_searches.htm. 21 November 2017.

2. Novik, Naomi. 1999. Blind Search Algorithms. http://cse.unl.edu/~choueiry/S03-476-876/searchapplet/. 21 November 2017.

3. Anonim. 1998. Blind Search-Part 2. http://web.cs.ucdavis.edu/~vemuri/classes/ecs170/search3b-blind.ppt. 21 November 2017.
4.  Zuse, Konrad. 1972. Der Plankalkül (The Formal System for Planning). http://zuse.zib.de/item/gHI1cNsUuQweHB6. 22 November 2017.
5. Moore, Edward F. 1959. The Shortest Path Through A Maze. Proceedings of the International Symposium on the Theory of Switching. Harvard University Press. pp. 285–292.
6. Wijanarto. Algoritma BFS dan DFS. http://eprints.dinus.ac.id/14269/1/slide_13b.pdf. 22 November 2017.
7. Anonim. 2015. Makalah Algoritma Breadth-First Search (BFS). http://yoursknowladge.blogspot.co.id/2015/04/makalah-algoritma-breadth-first-search.html. 22 November 2017
8. Even, Shimon (2011), Graph Algorithms (2nd ed.), Cambridge University Press, pp. 46–48
9. Herwanto, Arif dan Bambang Eka Purnama. 2013. Penerapan Metode Depth First Search pada Pencarian Rute Bus Kota Berbasis Web Mobile di Solo. Solo: Jurnal Ilmiah Go Infotech. Vol. 19, No. 1: 7-13.
10. Marcoulides, George A. 1998. Modern Methods for Business Research. Psychology Press. pp. 147–173
11. Tru, Cao Hoang. 2009. Heuristic Search - Part 3. http://www.cse.hcmut.edu.vn/~tru/AI/chapter3.pdf. 30 November 2017.
12. Welianto, Selvy dkk. 2011. Implementasi Algoritma Generate and Test Pada Pencarian Rute Terpendek. Yogyakarta: Jurnal Informatika . Vol. 7, No. 2: 1-10.
13. Anonim. 2017. Example of Hill Climbing Algorithm. http://www.baeldung.com/java-hill-climbing-algorithm. 5 Desember 2017.
14. Anonim. 2016. Contoh Pencarian Generate and Test. https://amandainhere.blogspot.co.id/2016/11/contoh-pencarian-generate-and-test.html.  6 Desember 2017.